写文章
  1. 码农之家首页
  2. 前端教程

字符串匹配 KMP 算法（详解指针回溯版）

我心飞翔 • • 前端教程 • 阅读 2

字符串匹配问题

这里直接采用 leetcode 28.找出字符串中第一个匹配项的下标的题干描述：

给你两个字符串 haystack 和 needle ，请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标（下标从 0 开始）。如果 needle 不是 haystack 的一部分，则返回  -1 。

 

示例 1：

输入： haystack = "sadbutsad", needle = "sad"
输出： 0
解释： "sad" 在下标 0 和 6 处匹配。
第一个匹配项的下标是 0 ，所以返回 0 。

示例 2：

输入： haystack = "leetcode", needle = "leeto"
输出： -1
解释： "leeto" 没有在 "leetcode" 中出现，所以返回 -1 。

在后面讲解中，我们一般把haystack称作主串，needle称作模式串。

暴力解法

暴力解法，思路很简单：

  • 两层循环，第一层循环遍历主串，第二层循环遍历模式串
  • 如果两个串当前索引下一致，就比对下一个索引。
  • 如果不一致，模式串索引归零；主串索引回溯到本次循环初始值，以进入下一次循环。
  • 如果模式串被遍历结束，说明主串中存在模式串，返回模式串初始位置 i-j
var strStr = function (haystack, needle) {
  for (let i = 0; i < haystack.length; i++) {
    let j = 0
    const initI = i
    while (j < needle.length) {
      if (haystack[i] === needle[j]) {
        i++;
        j++
      } else {
        i = initI // i回溯
        break
      }
    }
    if (j === needle.length) {
      return i - j
    }
  }
  return -1
}

kmp算法

上述暴力解法中存在一个很大的问题，就是在匹配失败时，没有利用其前面字符的成功经验。如下例中，在模式串匹配到最后一个字符f时失败了，但是前面的aabaa其实都是匹配成功的，这里一定是有信息可以利用的。

const content = 'aabaabaaf'
const pattern = 'aabaaf'

kmp算法就是这么一种算法，在匹配失败时，它利用之前匹配成功的数据，做到了主串指针不回溯，从而大大降低了算法复杂度。不过在开始说kmp算法之前，要先明确前后缀的概念

前缀（真前缀）

字符串的真前缀，指的是一个字符串中从开头开始的部分子串，但不包括整个字符串本身。换句话说，对于一个字符串，它的真前缀是从第一个字符开始，但不包括整个字符串的部分。

举个例子，对于字符串 “hello”，它的真前缀包括：”h”、”he”、”hel” 和 “hell”。
我们下文中说的前缀都是指真前缀，其中”hell”又叫最长前缀

后缀（真后缀）

字符串真后缀，指的是一个字符串中从末尾开始的部分子串，但不包括整个字符串本身。换句话说，对于一个字符串，它的真后缀是从最后一个字符开始，但不包括整个字符串的部分。

举个例子，对于字符串 “hello”，它的真后缀包括：”ello”、”llo”、”lo” 和 “o”。
我们下文中说的后缀都是指真后缀，其中”ello”又叫最长后缀

公共前后缀

一般来说公共前后缀(也可以叫相等前后缀)指的是在一段字符串中，某个子串，既是其前缀，又是其后缀。

举个例子，对于字符串”aabaa”：

  • 前缀包括：”a”、”aa”、”aab”、”aaba”。
  • 后缀包括：”a”、”aa”、”baa”、”abaa”。
  • 公共前后缀包括：”a”、”aa”
  • 其中”aa”是字符串”aabaa”的最长公共前后缀（最长相等前后缀）

如果是两个字符串，

kmp算法详解

例如主串叫content，模式串叫pattern,在暴力匹配进入到如下步骤时：
按照上述代码此时 initI = 2; i = 7; j = 5

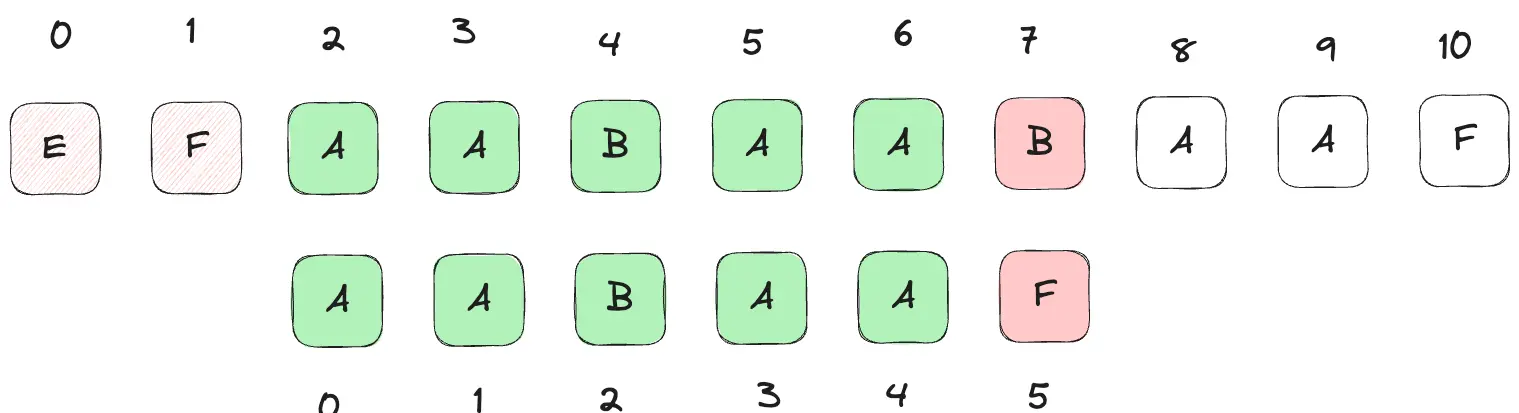
字符串匹配 KMP 算法（详解指针回溯版）

按照暴力匹配规则，由于此时content[7] !== pattern[5]，所以j要归零j = 0，i要回溯到本次外层循环的初始值i = initI // ->2，然后执行i++进入下一次循环。

kmp原理

不回溯i指针，只回溯j指针到必要的位置。其核心目的就是跳过尽可能多的无意义匹配。
当content[i] === pattern[j]时，和暴力解法相同，向前挪动两个指针。
当content[i] !== pattern[j]时，首先看之前位置上两者是否匹配。

  • 如果j === 0，不存在所谓的之前位置，j不能再回溯，和暴力解法相同，直接挪动i指针。
  • 如果j > 0，回退j指针nextJ到pattern[0, nextJ-1] === content[i-nextJ, i-1]时（如下图j从5回跳到2）。从而跳过content[i-nextJ]到content[i-1]这nextJ-1个字符的逻辑判断，继续回到第i个字符的判断逻辑：content[i] === pattern[nextJ]。
  • 这里为什么能跳过nextJ-1个字符的逻辑判断，可以理解成暴力算法中，i运行到initI = i-nextJ时，代入上个等式得pattern[0, nextJ-1] === content[initI, initI+nextJ-1]，即两个串content[initI, content.length-1]和pattern[0, pattern.length-1]有共同的前缀。那么共同前缀因为完全相同，自然是可以跳过匹配逻辑判断的。

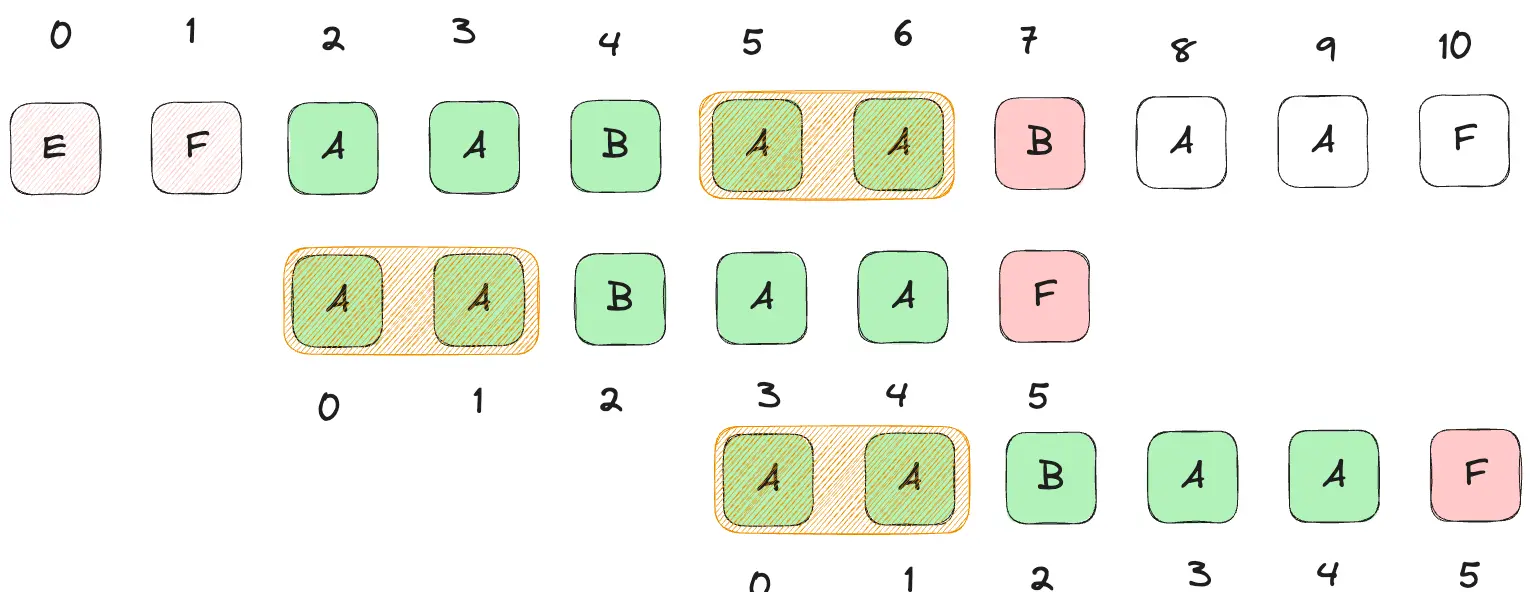
字符串匹配 KMP 算法（详解指针回溯版）
具体步骤和代码分析如下：

前提：

  1. 根据匹配规则，如果匹配到content[i]和pattern[j]时两个字符不相等，且j大于0，则content[initI,i-1]和pattern[0,j-1]一定相等。
  2. 目前已经准备好了一张pattern的最大公共前后缀长度表nextArr，其中pattern[0,i]的最大前后缀长度就是nextArr[i]。

具体执行逻辑

content[i] 和 pattern[j]相互比较，

  1. 在两者不相等且j>0(j可以回退)时：i不动，j回退为nextJ，使得j = nextJ重新进入content[i] 和 pattern[j]相互比较的逻辑。
    回退的原则如下：
    1）保证回退以后，模式串子串pattern[0, j-1]的前nextJ位和主串子串content[initI, i-1]后nextJ位相等。即pattern[0, nextJ-1] === content[i-nextJ, i-1]，因为只有他们相等，才能跳过他们，直接进入content[i] 和 pattern[nextJ]的比较。
    2）在保证原则1的情况下，nextJ应该尽量的大，因为nextJ越大，意味着跳过的无需匹配的元素越多。

    • 根据前提1的content[initI, i-1] === pattern[0, j-1]，可以把原则1中的content[i-nextJ, i-1]替换成pattern[j-nextJ, j-1]。具体替换原理如下：content[i-nextJ, i-1]的含义是倒数后nextJ位正序组成的子串，由于content[initI, i-1] === pattern[0, j-1]，两者倒数后nextJ位正序组成的子串就是相同的，后者相应子串为pattern[j-nextJ, j-1]。
    • 于是新的原则就诞生了：pattern[0, nextJ-1] === pattern[j-nextJ, j-1]，这个等式的含义就是找到一个位置nextJ，使得pattern[0,j-1]的前nextJ位组成的子串 和 后nextJ位组成的子串全等
    • nextJ又要尽量大，其最大时，就是公共前后缀最长时，所以 nextJ就是pattern[0, j-1]最长公共前后缀的长度。根据前提2，pattern[0, j-1]的最长公共前后缀的长度可以查表得出，即nextJ = nextArr[j-1]
    • j = nextJ，重新进入 content[i]和pattern[j]相互比较的逻辑

  2. 在两者相等时：i++;j++，挪动两个指针。

  3. 如果j等于0，不管两者是否相等，都不用再计算nextJ，因为此时j已经不能回退了。pattern[0,0]连前后缀都没有，更不可能有公共前后缀了。

  4. 如果两者不相等(此时j等于0)，只挪动i指针 i++，因为j已经回退到初始位置了。

  5. 直到pattern串被遍历结束(j = pattern.length)，返回此时pattern串在content中的起始索引。

  6. 如果主串遍历结束都没有找到完整模式串，返回 -1

以下是代码实现，


var strStr = function (content, pattern) {
  const nextArr = generateNext(pattern)
  let j = 0
  let i = 0
  while (i < content.length) {
    if (j > 0 && pattern[j] !== content[i]) {
    // 对应步骤一，回溯j，重新进入匹配判断逻辑
      j = nextArr[j - 1]
    } else {
      // 如果两者相等，挪动j指针
      if (pattern[j] === content[i]) j++
      
      // i已经处理完，挪动i指针
      i++

      if (pattern.length - j > content.length - i) {
        // 优化，可以不写，pattern剩余大于content剩余。
        return -1
      }

      if (j === pattern.length) {
        return i - j
      }

    }
  }

  return -1
};

最大公共前后缀表解析

上文中，j回退主要依据前提2中所提到的pattern的最大公共前后缀表。接下来我们再来明确下这个表代表的含义，然后求解该表。
next表（也称为部分匹配表）记录了模式串中每个位置的最长相同前缀后缀的长度。具体来说，next[i] 表示模式串中以第 i 个字符结尾的子串的最长相同前缀后缀的长度，即：
pattern[0, next[i]] === pattern[i-next[i], i]，next[i] === 0时，前面等式中是两个空串。

求解最大公共前后缀表

在求解前，先定义一些会使用到的变量及其初始值：

  • suffixIndex = 1，循环不变量，最长公共后缀的待匹配位置，同时[0, suffixIndex-1]代表已经处理完成的部分，[suffixIndex, pattern.length-1]为待处理部分。suffixIndex初始值不能为0，是因为等于0时，会和下面的最长公共前缀的待匹配初始位置重合，导致逻辑不好设计。
  • prefixMaxLen = 0，循环不变量，遍历过程中，最长公共前缀的长度，作为索引就指向最长公共前缀待匹配字符的位置。
  • next = [0]，next表，第一个元素没有前后缀，所以直接写入0，这里也是为了保证下一个要写入的索引和suffixIndex相同。

字符串匹配 KMP 算法（详解指针回溯版）

进入求解逻辑：：

  1. 进入求解逻辑，首先遍历pattern字符串，在遍历结束以后，求解结束，可以用for循环或者while循环，这里我个人更喜欢while循环，那么循环条件就是suffixIndex < pattern.length
  2. 进入循环逻辑以后，先判断前缀串和后缀串的下个位置是否相同。
  3. 如果pattern[prefixMaxLen] === pattern[suffixIndex]，意味着pattern[0, prefixMaxLen] === pattern[suffixIndex-prefixMaxLen, suffixIndex]，公共前后缀长度+1(prefixMaxLen++)，在next表中记录suffixIndex对应的这个新的公共前后缀长度，然后挪动suffixIndex指针，进入下一个字符的判断。示例的话，就是从上图进入到下图。

字符串匹配 KMP 算法（详解指针回溯版）

  1. 如果pattern[prefixMaxLen] !== pattern[suffixIndex]

    • 这个判断的含义是，pattern[0, prefixMaxLen] !== pattern[suffixIndex-prefixMaxLen, suffixIndex]，即当pattern[suffixIndex]作为后缀串的末尾，且后缀串长度为prefixMaxLen时，前缀串和后缀串不相同。

    • 由于prefixMaxLen时，前后缀不同， 那么next[suffixIndex]一定小于prefixMaxLen。即最大公共前后缀指针 prefixMaxLen 要回退(减少)到nextPrefixMaxLen。

    • 回退需要满足条件1：prefixMaxLen > 0，如果prefixMaxLen不大于0，那就没有回退的余地了。

    • 回退需要满足条件2：因为回退以后，就要进行pattern[nextPrefixMaxLen]和pattern[suffixIndex]字符的比对，所以前缀串的 前nextPrefixMaxLen-1位 和后缀串的 后nextPrefixMaxLen-1位 必须相等。即pattern[0, nextPrefixMaxLen-1] === pattern[suffix-nextPrefixMaxLen, suffix-1]

    • 在上面那个等式中，nextPrefixMaxLen最大时，其实就是pattern[0, suffix-1]的最长相同前后缀，即prefixMaxLen，由于我们是从prefixMaxLen开始回退的，所以nextPrefixMaxLen当然不能取prefixMaxLen的值，那么最长公共前后缀不能取，nextPrefixMaxLen的实际含义就是pattern[0, suffix-1]公共前后缀中第二长的公共前后缀的长度，我们也可以叫它次长相等前后缀的长度。但是根据目前得到的信息，可以列出如下等式。

      pattern[0, prefixMaxLen-1]     ===   pattern[suffix-prefixMaxLen, suffix-1]
pattern[0, nextPrefixMaxLen-1] ===   pattern[suffix-nextPrefixMaxLen, suffix-1]
nextPrefixMaxLen < prefixMaxLen

      将等式转换成示意图如下（最长相等前后缀是否重叠并不影响分析，为了便于演示，这里让其不重叠）：
      字符串匹配 KMP 算法（详解指针回溯版）

    • 根据上图，蓝色网状区域就是我们要求解的nextPrefixMaxLen，它需要尽可能的大。而且根据nextPrefixMaxLen < prefixMaxLen，它一定会小于绿色区域。由于两个蓝色区域一定相同(相等的前缀和后缀)，两个绿色区域也一定相同(相等的前缀和后缀)。我们可以把两个绿色区域重叠成一个(也可理解成把右侧的蓝色区域映射到左侧绿色区域中)，蓝色区域重合不重合并不影响分析，这里为了图示的清晰，让两个蓝色区域不出现重合。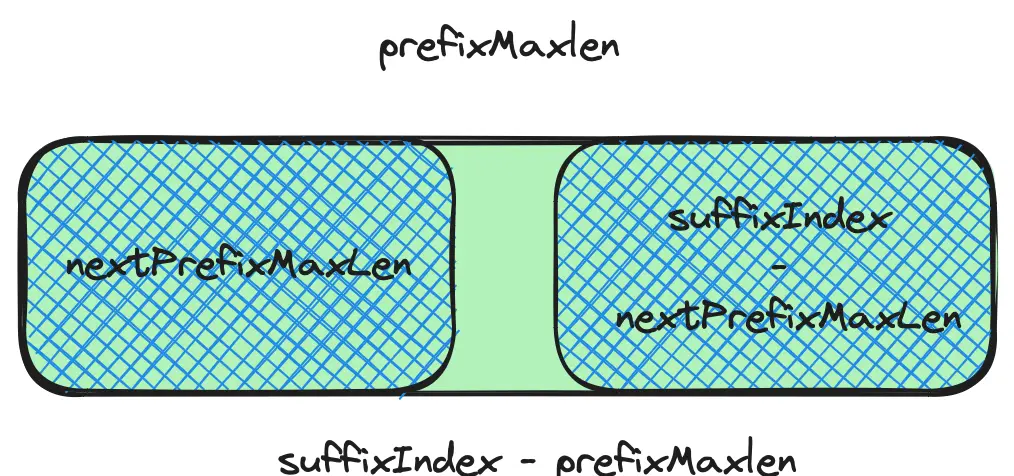
      字符串匹配 KMP 算法（详解指针回溯版）

    • 这里通过上图的演示，已经能看出来，nextPrefixMaxLen属于pattern[0, prefixMaxLen-1]的相等前后缀

    • 除了通过图分析外，还可以从实际语义角度分析。通过前缀和后缀的定义，得出如下两个结论：
      1）次长前缀一定属于最长前缀的前缀。因为两者都从 0 位置开始，后者长度更长。
      2）次长后缀一定属于最长后缀的后缀。因为两者都以 suffixIndex-1 位置终止，后者长度更长。
      而prefixMaxLen和nextPrefixMaxLen代表的都是pattern[0, suffixIndex-1]相等的前缀和后缀的长度，代入上述结论得到

      1. pattern[0, suffixIndex-1]的次长相等前缀(pattern[0, nextPrefixMaxLen-1])，一定属于其最长相等前缀(pattern[0, prefixMaxLen-1])的前缀

      2. pattern[0, suffixIndex-1]的次长相等后缀(pattern[0, nextPrefixMaxLen-1])，一定属于其最长相等后缀(pattern[suffix-prefixMaxLen,suffix-1])的后缀

      3. 由于最长相等前缀pattern[0, prefixMaxLen-1]和最长相等后缀pattern[suffix-prefixMaxLen,suffix-1]是相同的，所以可以把2中的最长相等后缀替换成最长相等前缀。于是得到：
        pattern[0, suffixIndex-1]的次长相等后缀(pattern[0, nextPrefixMaxLen-1])，一定属于其最长相等前缀(pattern[0, prefixMaxLen-1])的后缀

      4. 综合1和3得出，次长相等前缀一定是最长相等前缀的前缀，次长相等后缀一定是最长相等前缀的后缀，即：次长相等前后缀一定是最长相等前后缀对应字符串(pattern[0, prefixMaxLen-1])的相等前后缀，而这和上图分析的结果是一致的。

    • 又nextPrefixMaxLen需要尽可能大，所以nextPrefixMaxLen是pattern[0, prefixMaxLen-1]的最长相等前后缀。

    • 而pattern[0, prefixMaxLen-1]的最长相同前后缀的长度，已经在next表中记录过了，取出赋值即可：
      nextPrefixMaxLen = next[prefixMaxLen-1]
      步骤4结束，重新进入步骤2的逻辑判断。

  2. 如果(pattern[prefixMaxLen] !== pattern[suffixIndex]) && j === 0，这意味着j已经回溯到底了，但在pattern[0,suffixIndex]上，还是没有找到相等前后缀。在next表上记录next[suffixIndex] = 0，然后移动suffixIndex指针，进入下一个字符的处理。

最大公共前缀表代码实现

根据上面分析，可以得出如下代码，

function generateNext(str) {
  let prefixMaxLen = 0
  let next = [prefixMaxLen]
  let suffixIndex = 1
  while (suffixIndex < str.length) {
    if (str[prefixMaxLen] === str[suffixIndex]) {
      // 对应上面步骤3
      prefixMaxLen++
      next[suffixIndex] = prefixMaxLen
      suffixIndex++
    } else {
      if (prefixMaxLen > 0) {
        // 这里如果还不理解，多看几遍步骤4。
        // 寻找次长相等前后缀，而 次长相等前后缀 就是 最长相等前后缀本身 的 最长相等前后缀。
        prefixMaxLen = next[prefixMaxLen - 1]
      } else {
        // 步骤5
        next[suffixIndex] = 0
        suffixIndex++
      }
    }
  }
  return next
}

更简洁的代码实现

上面kmp算法和求解next数组的算法，为了便于讲解，实现起来没那么简洁，在了解其相应设计思想以后，不难写出如下实现

function getNext(pattern) {
  let next = new Array(pattern.length).fill(0)
  for (let i = 1, j = 0; i < pattern.length; i++) {
    while (j > 0 && pattern[i] !== pattern[j]) j = next[j - 1]
    next[i] = pattern[i] === pattern[j] ? ++j : j
  }
  return next
}

function kmpSearch(content, pattern) {
  const next = getNext(pattern)
  for (let i = 0, j = 0; i < content.length; i++) {
    while (j > 0 && content[i] !== pattern[j]) j = next[j - 1]
    if (content[i] === pattern[j]) j++
    if (pattern.length - j > content.length - i) return -1
    if (j === pattern.length) return i - j + 1
  }
  return -1
}

kmp算法正确性证明

看了下大佬们的计算，头发都不够掉的了，还是算了吧。
参考如下：

原文链接：https://juejin.cn/post/7347989108171538458 作者：Jeffrey0211

赞 (0)
我心飞翔我心飞翔
0 0
上一篇 2024年3月21日 下午5:08
下一篇 2024年3月22日 上午10:00

相关推荐

发表回复

登录后才能评论